Ranking method¶

Main task¶

Segmentation of the Aortic Vessel Tree¶

Together with the Dice Similarity Score (DSC) and Hausdorff Distance (HD), Sobol' sensitivity indices will be used to rank the submitted algorithms. The Sobol' indices will quantify the influence of image variation on the evaluation metrics, such as intensities, rotations, translations, noise, and blur. We will employ the first-order 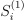and the total-order Sobol' indices . The former quantifies the influence of each input variability alone on the evaluation metrics (DSC, HD), and the latter quantifies the interaction between the variables on the variation of the evaluation metrics.

The challenge aims to provide a robust segmentation algorithm against each image variation. To ensure this, several criteria are considered:

On image variability¶

Evaluation metrics (DSC and HD) are to be equally influenced by each image variation to ensure a robust algorithm in all variations equally. This is measured with the first-order Sobol' indices of each image variation, such as:
 ,

where M is the total number of image variations. The closer p1 is to the unity, the more the distribution of the first-order Sobol' indices is uniform (ideal case).

On variability interaction¶

The algorithm should ensure that the influence of each image variation has no interaction with any other variation. This is measured with the difference between the total-order and first-order Sobol' indices, as given by
 .

The closer p2 is to zero, the less the amount of interaction between the variables is given by the algorithm.

Figure 1: Example of bad and good first- and total-order Sobol' indices for the 4 image variation variables: rotation, blur, intensity, and noise.

On Hausdorff distance metric¶

The evaluation metric HD must be characterized by a small variation with a value as close as possible to 0. Due to the skewed distribution of the computed HD, on each algorithm, the median (), the variance (), and the skewness () are included for the evaluation of the HD metric p3. The proposed evaluation metric encompasses multiple factors for a comprehensive assessment. Distinct performance dimensions are addressed by analyzing the median, variance, and skewness of result distributions. A ranking is formulated for each variable, providing insights into central tendency, spread, and asymmetry. The final metric synthesizes these rankings, employing weights that underscore their significance: 0.6 for median-based ranking, 0.25 for variance, and 0.15 for skewness. This weighted aggregation approach achieves A thorough assessment by factoring in many statistical attributes. The approach enhances the metric's sensitivity to various data characteristics, fostering a refined perspective on performance that goes beyond a singular measure.

 .

is the Fisher's moment coefficient of skewness of the HD distribution, computed on the mean and variance of the evaluation metric distribution. The weights are considered as = 0.6 , = 0.25, and = 0.15.

Figure 2: Example of 2 probability distribution functions (PDF) of the HD metric. The better PDF has a lower median, variance, and positive skewness parameters than the worse PDF.

On Dice Score metric¶

The evaluation metric DSC must be characterized by a small variation with a value as close as 1. The DSC evaluation methodology follows a similar approach to the HD metric. It involves assessing the median (), variance (), and skewness () of outcome distributions and ranking them accordingly. These rankings are then combined with weights of 0.6, 0.25, and 0.15 to create a balanced final metric p4 that captures various performance aspects.

.

Figure 3: Example of 2 probability distribution functions (PDF) of the DSC metric. The better PDF has a median closer to 1, lower variance, and lower negative skewness parameter than the worse PDF.

Final ranking¶

For each criterium, we produce an intermediate ranking. The weighted average gives the final computed ranking:

,

where the sensitivity analysis rankings are considered together as one contribution. In the case of equal ranking, the lowest average execution time is ranked higher.

SUBTASK 1 (optional)¶

Volumetric meshing of the Aortic Vessel Tree¶

The Jacobian evaluation methodology follows a similar approach to the previous metrics metric. It involves assessing the median (), variance (), skewness (), and the average number of invalid elements over all runs (characterized by a negative scaled Jacobian), defined as "n" of outcome distributions, and ranking them accordingly. These rankings are then combined with weights of 0.3, 0.25, 0.15, and 0.3 to create a balanced final metric pJ that captures various performance aspects.

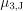where is the median, is the variance, and is the skewness of the scaled Jacobian distribution for one geometry. In case of two or more teams obtain the same score, we will rank higher the solutions with the smaller number of mesh elements.

Participation in this subtask will not be considered when the mean_jacobian value is equal to -100 in the generated .json file. Any other submitted value will be considered as active participation in subtask 1. When mean_jacobian value is -99, then it is considered as a valid result for subtask 1, but the volumetric mesh is probably affected by a tetgen generation error or is not watertight!

The ranking of this metric will be separated from the grand-challenge leaderboard. An updated leaderboard of this subtask will be updated regularly during Phase 2.

SUBTASK 2 (optional)¶

Surface meshing for visualization of the Aortic Vessel Tree¶

Surface mesh representations are evaluated by a team of two experienced medical professionals using a Likert-scale questionnaire. The qualitative evaluation will focus on the number of relevant branches and the presence of artifacts.

Participation in this subtask will be considered when the vis_available value is set to True.